Typ 1:
Es tritt nur eine trigonometrische Funktion mit ein und demselben Argument auf, z.B. 

Typ 2:
Es treten verschiedene trigonometrische Funktionen mit ein und demselben Argument auf, z.B.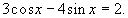 

Typ 3:
Es treten trigonometrische Funktionen mit verschiedenen Argumenten auf, z.B.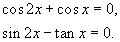 

Grundsätzlicher Lösungsweg:

1. Anwendung goniometrischer Formeln mit dem Ziel, die Gleichung bis zum Typ 1 zu vereinfachen.
2. In Gleichungen vom Typ 1 wird, falls das notwendig ist, der trigonometrische Term durch eine algebraische Größe substituiert, die verbleibende algebraische Gleichung gelöst und die Rücksubstitution durchgeführt.
3. Die Lösungen der verbleibenden goniometrischen Gleichungen der Form 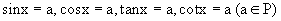können sofort mit Hilfe eines geeigneten Rechenhilfsmittels bestimmt werden. Beachten Sie dabei, dass zwei Möglichkeiten bestehen:
Entweder ist die Lösungsmenge leer (z.B. sin x = 2), oder es treten wegen der Periodizität der Winkelfunktionen mit einer Lösung unendlich viel weitere Lösungen auf. Oft wird durch Angabe des Grundbereiches die Anzahl der Lösungen eingeschränkt
(z.B. °).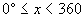
4. Es können Ergebnisse auftreten, welche die gegebenen Gleichung nicht erfüllen. Das ist der Fall, wenn quadriert werden muss (nichatäquvalente Umformung). In solchen Fällen ist es notwendig, die Probe durchzuführen. Wir empfehlen Ihnen, die Probe grundsätzlich durchzuführen.