Zu bestimmen ist die Lösungsmenge der Gleichung

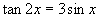(Typ 3).

Lösungsweg:

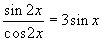1. nach (17)

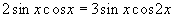   nach (21)

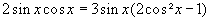   nach (22)

   Umordnen und sin x ausklammern:

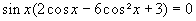   (Typ 2)

   Ein Produkt ist genau dann gleich 0, wenn mindestens ein Faktor 0 ist, also wenn

   1. sin x = 0 oder
   2. 
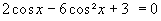
   ist.
   Die Gleichungen I. und II. sind vom Typ 1.

2. Da Gleichung II quadratisch in cos x ist, wird zunächst cos x = z substituiert.
   Es entsteht die Normalform ...... .
   Die Lösung dieser Gleichung sind z₁ = 0,8932 und z₂ = ......... . 
   Durch die Rücksubstitution ergeben sich die Gleichungen cos x = 0,8932 und .........

3. Die verbleibenden Gleichungen liefern die Lösungen

   sin x =0 

   cos x=0,8932 

   cos x=.......... 

4. Die Probe für x=26,7°+k*360° ergibt:
Linke Seite: tan2 (26,7°+k*360°)=tan53,4°=1,347

Rechte Seite: 3sin (26,7°+k*360°)=3sin26,7°=1,348.