Verzweigte Programme

Struktogramm:

Erklärung:
Es wird geprüft, ob die Bedingung wahr oder falsch ist.
Ist sie wahr, so wird der Anweisungsblock 1 abgearbeitet. Sollte sie jedoch falsch sein, so wird der Anweisungsblock 2 durchgeführt.

Syntax:

if (Bedingung)
{
  Anweisungsblock 1
}
else
{
  Anweisungsblock 2
{

Beispiel:

if (nenner != 0 )
{
  bruch = zaehler / nenner;
  cout << "Bruch hat den Wert " << bruch;
}
else
{
  cout << "Der Bruch ist nicht definiert!";
}

Struktogramm:

Erklärung:
Es wird geprüft, ob die Bedingung wahr oder falsch ist.
Ist sie wahr, so wird der Anweisungsblock abgearbeitet. Sollte sie jedoch falsch sein, so wird nichts durchgeführt.

Syntax:

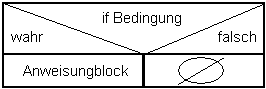
if (Bedingung)
{
  Anweisungsblock
}

Beispiel:

if (password == "x6y3z")
{
  cout << "Passwort ist OK!";
}

Wenn der Anweisungsblock aus nur einer Anweisung besteht, kann sie auch ohne geschweifte Klammern geschrieben werden.

if (password == "x6y3z") cout << "Passwort ist OK!";

Jede Bedingung ist eine Aussage. Bedingungen können auch logisch verknüpft werden. Diese Verknüpfung ist wieder eine Aussage.

Beispiel:

a ist nicht größer als b oder b ist größer als c

Durch aussagenlogische Gesetze lassen sich solche verknüpften Bedingungen häufig vereinfachen

Die Negation (Verneinung) einer Aussage

Man bezeichnet eine Aussage meist mit einem Großbuchstaben. Die Negation einer Aussage bezeichnet man, indem man über den Großbuchstaben einen Strich macht.

Beispiel:

Aussage A --> Negation

Es gilt das Gesetz der doppelten Verneinung:
Das heißt z.B.: "Es kann nicht sein, dass a nicht kleiner als b ist." ist logisch gleichbedeutend mit "a ist kleiner als b."
Logisch oder???

Die Konjunktion (Und-Verknüpfung) zweier Aussagen

Die Konjunktion zweier Aussagen bezeichnet man, indem man zwischen die Aussagen ein (logisches Und) setzt.

Beispiel:

Aussage A und B --> Konjunktion

Es gilt das Kommutativgesetz:
Das heißt z.B.: "a < b und b < c" ist logisch gleichbedeutend mit "b < c und a < b"
Auch logisch oder???

Die Disjunktion (Oder-Verknüpfung) zweier Aussagen

Die Disjunktion zweier Aussagen bezeichnet man, indem man zwischen die Aussagen ein (logisches Oder) setzt.

Beispiel:

Aussage A oder B --> Disjunktion

Es gilt auch das Kommutativgesetz:
Das heißt z.B.: "a < b oder b < c" ist logisch gleichbedeutend mit "b < c oder a < b"
Wieder logisch oder???

Um die Gesetze zu beweisen, stellt man die zugehörigen Warheitswerttabellen auf.
Lade dir dazu die Excel-Datei Wahrheitswerttabellen_Vorlage.xls herunter.
Ergänze die entsprechenden Formeln. Beachte dabei, dass bei den logischen Excel-Funktionen der Verknüpfungsoperator der Funktionsname ist. Der jeweiligen Funktion werden die Wahrheitswerte der entsprechenden Aussagen als Parameter übergeben. Mehrere Parameter müssen durch ein ";" getrennt werden.
Dadurch sieht das Ganze etwas seltsam aus.

Zur Kontrolle kannst du deine Lösung mit der Datei Wahrheitswerttabellen_Loesung.xls vergleichen.
Wie du siehst, stimmen bei allen Gesetzen die linke Spalte mit der rechten Spalte überein. Damit sind die Gestze bewiesen.